Линии первого порядка примеры. Линии второго порядка на плоскости

Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.

Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F - числа и хотя бы один из коэффициентов A, B, C не равен нулю.

При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.

Эллипс, заданный каноническим уравнением

Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.

Фокусы обозначены как и на рисунке ниже.

Каноническое уравнение эллипса имеет вид:

где a и b (a > b ) - длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.

Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.

Ось абсцисс эллипс пересекает в точках (a , О ) и (- a , О ), а ось ординат - в точках (b , О ) и (- b , О ). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат - малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность - частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a /b раз вдоль оси Oy .

Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.

Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:

Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия - эллипс.

Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.

Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось - это a = 5 , меньшая полуось - это b = 4 . Получаем каноническое уравнение эллипса:

Точки и , обозначенные зелёным на большей оси, где

называются фокусами .

называется эксцентриситетом эллипса.

Отношение b /a характеризует "сплюснутость" эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.

Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.

Решение. Делаем несложные умозаключения:

Если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,

Если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.

Подставляем и вычисляем:

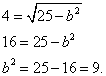
Результат - каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .

Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c , нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:

Составляем каноническое уравнение эллипса:

Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .

Решение. Следует найти число c , определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) расстояние между фокусами 30, а большая ось 34

2) малая ось 24, а один из фокусов находится в точке (-5; 0)

3) эксцентриситет , а один из фокусов находится в точке (6; 0)

Продолжаем решать задачи на эллипс вместе

Если - произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и - расстояния до этой точки от фокусов , то формулы для расстояний - следующие:

Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a .

Прямые, определяемые уравнениями

называются директрисами эллипса (на чертеже - красные линии по краям).

Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где и - расстояния этой точки до директрис и .

Пример 7. Дан эллипс . Составить уравнение его директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:

Получаем уравнение директрис эллипса:

Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .

11.1. Основные понятия

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

Коэффициенты уравнения - действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Ниже будет установлено, что уравнение (11.1) определяет на плоскости окружность, эллипс, гиперболу или параболу. Прежде, чем переходить к этому утверждению, изучим свойства перечисленных кривых.

11.2. Окружность

Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R с центром в точке называется множество всех точек Μ плоскости, удовлетворяющих условию . Пусть точка в прямоугольной системе координат имеет координаты x 0 , y 0 а - произвольная точка окружности (см. рис. 48).

Тогда из условия получаем уравнение

(11.2)

Уравнению (11.2) удовлетворяют координаты любой точки данной окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности.

Уравнение (11.2) называется каноническим уравнением окружности

В частности, полагая и , получим уравнение окружности с центром в начале координат .

Уравнение окружности (11.2) после несложных преобразований примет вид . При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:

1) коэффициенты при x 2 и у 2 равны между собой;

2) отсутствует член, содержащий произведение xу текущих координат.

Рассмотрим обратную задачу. Положив в уравнении (11.1) значения и , получим

Преобразуем это уравнение:

(11.4)

Отсюда следует, что уравнение (11.3) определяет окружность при условии . Ее центр находится в точке , а радиус

Если же , то уравнение (11.3) имеет вид

Ему удовлетворяют координаты единственой точки . В этом случае говорят: “окружность выродилась в точку” (имеет нулевой радиус).

Если , то уравнение (11.4), а следовательно, и равносильное уравнение (11.3), не определят никакой линии, так как правая часть уравнения (11.4) отрицательна, а левая – не отрицательная (говорять: “окружность мнимая”).

11.3. Эллипс

Каноническое уравнение эллипса

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами , есть величина постоянная, большая, чем расстояние между фокусами.

Обозначим фокусы через F 1 и F 2 , расстояние между ними через 2c , а сумму расстояний от произвольной точки эллипса до фокусов - через 2a (см. рис. 49). По определению 2a > 2c , т. е. a > c .

Для вывода уравнения эллипса выберем систему координат так, чтобы фокусы F 1 и F 2 лежали на оси , а начало координат совпадало с серединой отрезка F 1 F 2 . Тогда фокусы будут иметь следующие координаты: и .

Пусть - произвольная точка эллипса. Тогда, согласно определению эллипса, , т. е.

Это, по сути, и есть уравнение эллипса.

Преобразуем уравнение (11.5) к более простому виду следующим образом:

Так как a >с , то . Положим

(11.6)

Тогда последнее уравнение примет вид или

(11.7)

Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническимуравнением эллипса .

Эллипс - кривая второго порядка.

Исследование формы эллипса по его уравнению

Установим форму эллипса, пользуясь его каноническим уравнением.

1. Уравнение (11.7) содержит х и у только в четных степенях, поэтому если точка принадлежит эллипсу, то ему также принадлежат точки ,,. Отсюда следует, что эллипс симметричен относительно осей и , а также относительно точки , которую называют центром эллипса.

2. Найдем точки пересечения эллипса с осями координат. Положив , находим две точки и , в которых ось пересекает эллипс (см. рис. 50). Положив в уравнении (11.7) , находим точки пересечения эллипса с осью : и . Точки A 1 , A 2 , B 1 , B 2 называются вершинами эллипса . Отрезки A 1 A 2 и B 1 B 2 , а также их длины 2a и 2b называются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.

3. Из уравнения (11.7) следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства и или и . Следовательно, все точки эллипса.лежаї внутри прямоугольника, образованного прямыми .

4. В уравнении (11.7) сумма неотрицательных слагаемых и равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если возрастает, то уменьшается и наоборот.

Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).

Дополнительные сведения об эллипсе

Форма эллипса зависит от отношения . При эллипс превращается в окружность, уравнение эллипса (11.7) принимает вид . В качестве характеристики формы эллипса чаще пользуются отношением . Отношение половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и o6oзначается буквой ε («эпсилон»):

причем 0<ε< 1, так как 0<с<а. С учетом равенства (11.6) формулу (11.8) можно переписать в виде

Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить ε = 0, то эллипс превращается в окружность.

Пусть М(х;у) -- произвольная точка эллипса с фокусами F 1 и F 2 (см. рис. 51). Длины отрезков F 1 M=r 1 и F 2 M = r 2 называются фокальными радиусами точки Μ. Очевидно,

Имеют место формулы

Прямые называются

Теорема 11.1. Если - расстояние от произвольной точки эллипса до какого-нибудь фокуса, d - расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение есть постоянная величина, равная эксцентриситету эллипса:

Из равенства (11.6) следует, что . Если же , то уравнение (11.7) определяет эллипс, большая ось которого лежит на оси Оу, а малая ось - на оси Ох (см. рис. 52). Фокусы такого эллипса находятся в точках и , где .

11.4. Гипербола

Каноническое уравнение гиперболы

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами , есть величина постоянная, меньшая, чем расстояние между фокусами.

Обозначим фокусы через F 1 и F 2 расстояние между ними через 2с , а модуль разности расстояний от каждой точки гиперболы до фокусов через 2a . По определению 2a < 2с , т. е. a < c .

Для вывода уравнения гиперболы выберем систему координат так, чтобы фокусы F 1 и F 2 лежали на оси , а начало координат совпало с серединой отрезка F 1 F 2 (см. рис. 53). Тогда фокусы будут иметь координаты и

Пусть - произвольная точка гиперболы. Тогда согласно определению гиперболы или , т.е.. После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы

(11.9)

(11.10)

Гипербола есть линия второго порядка.

Исследование формы гиперболы по ее уравнению

Установим форму гиперболы, пользуясь ее каконическим уравнением.

1. Уравнение (11.9) содержит x и у только в четных степенях. Следовательно, гипербола симметрична относительно осей и , а также относительно точки , которую называют центром гиперболы.

2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (11.9), находим две точки пересечения гиперболы с осью : и . Положив в (11.9), получаем , чего быть не может. Следовательно, гипербола ось Оу не пересекает.

Точки и называются вершинами гиперболы, а отрезок

действительной осью , отрезок - действительной полуосью гиперболы.

Отрезок , соединяющий точки и называется мнимой осью , число b - мнимой полуосью . Прямоугольник со сторонами 2a и 2b называется основным прямоугольником гиперболы .

3. Из уравнения (11.9) следует, что уменьшаемое не меньше единицы т. е. что или . Это означает, что точки гиперболы расположены справа от прямой (правая ветвь гиперболы) и слева от прямой (левая ветвь гиперболы).

4. Из уравнения (11.9) гиперболы видно, что когда возрастает, то и возрастает. Это следует из того, что разность сохраняет постоянное значение, равное единице.

Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 54 (кривая, состоящая из двух неограниченных ветвей).

Асимптоты гиперболы

Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой K до этой прямой стремится к нулю при неограниченном удалении точки M вдоль кривой K от начала координат. На рисунке 55 приведена иллюстрация понятия асимптоты: прямая L является асимптотой для кривой К.

Покажем, что гипербола имеет две асимптоты:

(11.11)

Так как прямые (11.11) и гипербола (11.9) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти.

Возьмем на прямой точку N имеющей ту же абсциссу х, что и точка на гиперболе (см.рис. 56), и найдем разность ΜΝ между ординатами прямой и ветви гиперболы:

Как видно, по мере возрастания х знаменатель дроби увеличивается; числитель - есть постоянная величина. Стало быть, длина отрезка ΜΝ стремится к нулю. Так как ΜΝ больше расстояния d от точки Μ до прямой, то d и подавно стремится к нулю. Итак, прямые являются асимптотами гиперболы (11.9).

При построении гиперболы (11.9) целесообразно сначала построить основной прямоугольник гиперболы (см. рис. 57), провести прямые, проходящие через противоположные вершины этого прямоугольника, - асимптоты гиперболы и отметить вершины и , гиперболы.

Уравнение равносторонней гиперболы.

асимптотами которой служат оси координат

Гипербола (11.9) называется равносторонней, если ее полуоси равны (). Ее каноническое уравнение

(11.12)

Асимптоты равносторонней гиперболы имеют уравнения и и, следовательно, являются биссектрисами координатных углов.

Рассмотрим уравнение этой гиперболы в новой системе координат (см. рис. 58), полученной из старой поворотом осей координат на угол . Используем формулы поворота осей координат:

Подставляем значения х и у в уравнение (11.12):

Уравнение равносторонней гиперболы, для которой оси Ох и Оу являются асимптотами, будет иметь вид .

Дополнительные сведения о гиперболе

Эксцентриситетом гиперболы (11.9) называется отношение расстояния между фокусами к величине действительной оси гиперболы, обозначается ε:

Так как для гиперболы , то эксцентриситет гиперболы больше единицы: . Эксцентриситет характеризует форму гиперболы. Действительно, из равенства (11.10) следует, что т.е. и .

Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение - ее полуосей, а значит, тем более вытянут ее основной прямоугольник.

Эксцентриситет равносторонней гиперболы равен . Действительно,

Фокальные радиусы и для точек правой ветви гиперболы имеют вид и , а для левой - и .

Прямые - называются директрисами гиперболы. Так как для гиперболы ε > 1, то . Это значит, что правая директриса расположена между центром и правой вершиной гиперболы, левая - между центром и левой вершиной.

Директрисы гиперболы имеют то же свойство , что и директрисы эллипса.

Кривая, определяемая уравнением также есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2a - на оси Ох. На рисунке 59 она изображена пунктиром.

Очевидно, что гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными.

11.5. Парабола

Каноническое уравнение параболы

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0).

Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директрисой (см. рис. 60). В выбранной системе фокус F имеет координаты , а уравнение директрисы имеет вид , или .

1. В уравнении (11.13) переменная у входит в четной степени, значит, парабола симметрична относительно оси Ох; ось Ох является осью симметрии параболы.

2. Так как ρ > 0, то из (11.13) следует, что . Следовательно, парабола расположена справа от оси Оу.

3. При имеем у = 0. Следовательно, парабола проходит через начало координат.

4. При неограниченном возрастании x модуль у также неограниченно возрастает. Парабола имеет вид (форму), изображенный на рисунке 61. Точка О(0; 0) называется вершиной параболы, отрезок FM = r называется фокальным радиусом точки М.

Уравнения , , (p>0 ) также определяют параболы, они изображены на рисунке 62

Нетрудно показать, что график квадратного трехчлена , где , B и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.

11.6. Общее уравнение линий второго порядка

Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям

Найдем сначала уравнение эллипса с центром в точке , оси симметрии которого параллельны координатным осям Ох и Оу и полуоси соответственно равны a и b . Поместим в центре эллипса O 1 начало новой системы координат , оси которой и полуосями a и b (см. рис. 64):

И, наконец, параболы, изображенные на рисунке 65, имеют соответствующие уравнения.

Уравнение

Уравнения эллипса, гиперболы, параболы и уравнение окружности после преобразований (раскрыть скобки, перенести все члены уравнения в одну сторону, привести подобные члены, ввести новые обозначения для коэффициентов) можно записать с помощью единого уравнения вида

где коэффициенты А и С не равны нулю одновременно.

Возникает вопрос: всякое ли уравнение вида (11.14) определяет одну из кривых (окружность, эллипс, гипербола, парабола) второго порядка? Ответ дает следующая теорема.

Теорема 11.2 . Уравнение (11.14) всегда определяет: либо окружность (при А = С), либо эллипс (при А · С > 0), либо гиперболу (при А · С < 0), либо параболу (при А×С= 0). При этом возможны случаи вырождения: для эллипса (окружности) - в точку или мнимый эллипс (окружность), для гиперболы - в пару пересекающихся прямых, для параболы - в пару параллельных прямых.

Общее уравнение второго порядка

Рассмотрим теперь общее уравнение второй степени с двумя неизвестными:

Оно отличается от уравнения (11.14) наличием члена с произведением координат (B¹ 0). Можно, путем поворота координатных осей на угол a , преобразовать это уравнение, чтобы в нем член с произведением координат отсутствовал.

Используя формулы поворота осей

выразим старые координаты через новые:

Выберем угол a так, чтобы коэффициент при х" · у" обратился в нуль, т. е. чтобы выполнялось равенство

Таким образом, при повороте осей на угол а, удовлетворяющий условию (11.17), уравнение (11.15) сводится к уравнению (11.14).

Вывод : общее уравнение второго порядка (11.15) определяет на плоскости (если не считать случаев вырождения и распадения) следующие кривые: окружность, эллипс, гиперболу, параболу.

Замечание: Если А = С, то уравнение (11.17) теряет смысл. В этом случае cos2α = 0 (см. (11.16)), тогда 2α = 90°, т. е. α = 45°. Итак, при А = С систему координат следует повернуть на 45°.

В декартовых координатах уравнение первой степени определяет некоторую прямую.

Линии, которые в декартовых координатах определяются уравнением первой степени, называются линиями первого порядка. Следовательно, каждая прямая есть линия первого порядка.

Общее уравнение прямой (как общее уравнение первой степени) определяется уравнением вида:

Ах + Ву + С = 0.

Рассмотрим неполные уравнения прямой.

1. С = 0. Уравнение прямой имеет вид: Ах + Ву = 0; прямая проходит через начало координат.

2. В = 0 (А ¹ 0). Уравнение имеет вид Ах + С = 0 или х = а , где а = Прямая проходит через точку А (а ; 0),она параллельна оси Оу . Число а Ох (рис. 1).

Рис. 1

Если а = 0, то прямая совпадает с осью Оу . Уравнение оси ординат Оу имеет вид : х = 0.

3. А = 0 (В ¹ 0). Уравнение имеет вид: Ву + С = 0 или у = b , где b = . Прямая проходит через точку В (0; b ),она параллельна оси Ох . Число b есть величина отрезка, который отсекает прямая на оси Оу (рис. 2).

Рис. 2

Если b = 0, то прямая совпадает с осью абсцисс Ох. Уравнение оси абсцисс Ох имеет вид: у = 0.

Уравнение прямой в отрезках на осях определяется уравнением:

Где числа а и b являются величинами отрезков, отсекаемых прямой на координатных осях (рис. 3).

(х 0 ; у 0) перпендикулярно нормальному вектору = {A ; B }, определяется по формуле:

А (х – х 0) + В (у – у 0) = 0.

Уравнение прямой, проходящей через данную точку М (х 0 ; у 0) параллельно направляющему вектору = {l ; m }, имеет вид:

Уравнение прямой, проходящей через две данные точки М 1 (х 1 ; у 1) и М 2 (х 2 ; у 2), определяется уравнением:

Угловым коэффициентом прямой k называется тангенс угла наклона прямой к оси Ох , который отсчитывается от положительного направления оси к прямой против часовой стрелки, k = tgα.

Уравнение прямой с угловым коэффициентом k имеет вид:

у = kх + b ,

где k = tgα, b – величина отрезка, отсекаемого прямой на оси Оу (рис. 4).

Уравнение прямой, проходящей через данную точку М (х 0 ; у 0) в данном направлении (угловой коэффициент k известен), определяется по формуле:

у – у 0 = k (х – х 0).

Уравнение пучка прямых, проходящих через данную точку М (х 0 ; у 0) (угловой коэффициент k неизвестен), определяется по формуле:

у – у 0 = k (х – х 0).

Уравнение пучка прямых, проходящих через точку пересечения прямых

А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0, определяется по формуле:

α(А 1 х + В 1 у + С 1) + β(А 2 х + В 2 у + С 2) = 0.

Угол j, отсчитанный против часовой стрелки от прямой у = k 1 х + b 1 к прямой у = k 2 х + b 2 , определяется формулой (рис. 5):

Для прямых, заданных общими уравнениями А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0, угол между двумя прямыми определяется по формуле:

Условие параллельности двух прямых имеет вид : k 1 = k 2 или .

Условие перпендикулярности двух прямых имеет вид : или А 1 А 2 + В 1 В 2 = 0.

Нормальное уравнение прямой имеет вид :

x cosα + y sinα – p = 0,

где p – длина перпендикуляра, опущенного из начала координат на прямую, α – угол наклона перпендикуляра к положительному направлению оси Ох (рис. 6).

Чтобы привести общее уравнение прямой Ах + Ву + С = 0 к нормальному виду, нужно все его члены умножить на нормирующий множитель μ = , взятый со знаком, противоположным знаку свободного члена С .

Расстояние от точки М (х 0 ; у 0) до прямой Ах + Ву + С = 0 определяется по формуле:

Уравнения биссектрис углов между прямыми А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0 имеют вид:

Пример 4 . Даны вершины треугольника АВС : А (–5; –7), В (7; 2), С (–6; 8). Найти: 1) длину стороны АВ ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол В ; 4) уравнение медианы АЕ ; 5) уравнение и длину высоты СD ; 6) уравнение биссектрисы АК ; 7) уравнение прямой, проходящей через точку Е параллельно стороне АВ ; 8) координаты точки М , расположенной симметрично точке А относительно прямой СD .

1. Расстояние d между двумя точками А (х 1 ; у 1) и В (х 2 ; у 2) определяется по формуле:

Найдем длину стороны АВ как расстояние между двумя точками А (–7; –8) и В (8; –3):

2. Уравнение прямой, проходящей через точки А (х 1 ; у 1) и В (х 2 ; y 2), имеет вид:

Подставляя координаты точек А и В , получим уравнение стороны АВ :

3(х + 5) = 4(у + 7); 3х – 4у – 13 = 0 (AВ ).

Для нахождения углового коэффициента k AB прямой (АВ ) разрешим полученное уравнение относительно у :

4y = 3x – 13;

– уравнение прямой (АВ )с угловым коэффициентом,

Аналогично подставляя координаты точек В и С , получим уравнение прямой (ВС ):

6х – 42 = –13у + 26; 6x + 13y – 68 = 0 (BC ).

Разрешим уравнение прямой (ВС )относительно у : .

3. Тангенс угла j между двумя прямыми, угловые коэффициенты которых равны k 1 и k 2 , определяется по формуле:

Внутренний угол В образован прямыми (АВ ) и (ВС ), причем это острый угол, на который надо повернуть прямую ВС в положительном направлении (против часовой стрелки) до ее совпадения с прямой (АВ ). Поэтому подставим в формулу k 1 = , k 2 = :

ÐВ = arctg = arctg 1,575 » 57,59°.

4. Чтобы найти уравнение медианы (АЕ ), определим сначала координаты точки Е, которая является серединой стороны ВС. Для этого применим формулы деления отрезка на две равные части:

Следовательно, точка Е имеет координаты: Е (0,5; 5).

Подставляя в уравнение прямой, проходящей через две точки, координаты точек А и Е , находим уравнение медианы (АЕ ):

24х – 11у + 43 = 0 (АЕ ).

5. Так как высота CD перпендикулярна стороне АВ , то прямая (АВ )перпендикулярна прямой (CD ). Для нахождения углового коэффициента высоты CD, воспользуемся условием перпендикулярности двух прямых:

Уравнение прямой, проходящей через данную точку М (х 0 ; у 0) в заданном направлении (угловой коэффициент k известен), имеет вид:

y – у 0 = k (x – x 0).

Подставляя в последнее уравнение координаты точки С (–6; 8) и , получим уравнение высоты CD :

у – 8 = (х – (–6)), 3у – 24 = – 4х – 24, 4х + 3у = 0 (CD ).

Расстояние от точки М (х 0 ; у 0) до прямой Аx + By+C = 0 определяется по формуле:

Длину высоты CD найдем как расстояние от точки С (–6; 8) до прямой (АВ ): 3х – 4у – 13. Подставляя в формулу необходимые величины, найдем длину CD :

6. Уравнения биссектрис углов между прямыми Аx + By+ C = 0 и
А 1 x + B 1 y+ C 1 = 0 определяются по формуле:

Уравнение биссектрисы АК найдем как одно из уравнений биссектрис углов между прямыми (АВ )и (АС ).

Составим уравнение прямой (АС ) как уравнение прямой, проходящей через две точки А (–5; –7) и С (–6; 8):

Преобразуем последнее уравнение:

15(х + 5) = – (у + 7); 15х + у + 82 = 0 (AС ).

Подставляя коэффициенты из общих уравнений прямых (АВ )и (АС ), получим уравнения биссектрис углов:

Преобразуем последнее уравнение:

; (3х – 4у – 13) = ± 5 (15х + у + 82);

3 х – 4 у – 13 = ± (75х +5у + 410).

Рассмотрим два случая:

1) 3 х – 4 у – 13 = 75х +5у + 410.у l АВ .

Треугольник АВС, высота CD , медиана АЕ , биссектриса АК , прямая l и точка М построены в системе координат Оху (рис.7).

Окружностью называется совокупность всех точек плоскости, равноудаленных от одной данной точки, называемой центром окружности. Расстояние от центра окружности до любой точки на окружности называется. радиусом окружности.

- каноническое уравнение окружности(16) - центр окружности.

Если центр окружности лежит в начале координат, то уравнение окружности (16 .)

Эллипсом называется совокупность всех точек плоскости, сумма расстояний которых от двух данных точек этой плоскости (называемых фокусами этого эллипса) есть величина постоянная.

В (0;b)M(x,y)

r 1 r 2 r 1 +r 2 =2a

(-а;0) F 1 (-c;0) 0 F 2 (c;0) (а;0) X

Обозначим для краткости a 2 -b 2 =c 2 (*), тогда уравнение эллипса: (17)

Если положить y=0, то получается , а если положить х=0, получается ; значит, и - это длины полуосей эллипса – большой () и малой (). Кроме того, каждое из слагаемых в левой части не может быть больше единицы, откуда , , и потому весь эллипс расположен внутри прямоугольника. Точки A,B,C,D, в которых эллипс пересекается своими осями симметрии, называются вершинами эллипса.

Отношение называется эксцентриситетом эллипса.

Гиперболой называется совокупность всех точек плоскости, модуль разности расстояний которых от двух данных точек этой плоскости (называемых фокусами этой гиперболы) есть величина постоянная. Середина расстояния между фокусами называется центром гиперболы .

r 2 r 1 –r 2 =2a

F 1 (-c;0) 0 F 2 (c;0) x

Обозначим a 2 -c 2 =-b 2 (**),уравнение гиперболы: (18)

Из этого уравнения видно, что и гипербола имеет две оси симметрии (главные оси), а так же центр симметрии (центр гиперболы).

Отношение называется эксцентриситетом гиперболы.

Если положить y=0, то получается , а если положить х=0, получается .

Значит ось Ох пересекает гиперболу в двух точках (вершинах гиперболы), это – вещественная ось ; Ось Оу гиперболу не пересекает – это «мнимая ось . » Всякий отрезок, соединяющий две точки гиперболы, если он проходит через центр, называется диаметром гиперболы.

Прямая, к которой кривая линия приближается сколь угодно близко, но никогда не пересекает ее называется асимптотой кривой. Гипербола имеет две асимптоты. Их уравнения: (19)

Параболой называется совокупность всех точек плоскости расстояние от каждой из которых до данной точки (называемой фокусом) равно расстоянию до данной прямой (называемой директрисой) .

- параметр параболы.

Парабола имеет одну ось симметрии. Точка пересечения параболы с осью симметрии называется вершиной параболы .

Каноническое уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Ох и ветви направлены вправо имеет вид (20)

Уравнение ее директрисы:

Каноническое уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Ох и ветви направлены влево имеет вид (20 ,)

Уравнение ее директрисы:

Каноническое уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Оу и ветви направлены вверх имеет вид (20 ,)

Уравнение ее директрисы:

Каноническое уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Оу и ветви направлены вниз имеет вид (20 ,)

Уравнение ее директрисы:

y y

F 0 p/2 x -p/2 0 x

Y y

p/2

–p/2
Тема 2.1. Лекция 7.Занятие 10

Тема: Функции одной независимой переменной, их графики.

Понятие функции

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.

Пусть даны два непустых множества X и Y. Соответствие ƒ, которое каждому элементу хÎ X сопоставляет один и только один элемент уÎ Y, называется функцией и записывается у=ƒ(х), хÎ X или ƒ: X→Y. Говорят еще, что функция ƒ отображает множество X на множество Y.

Например, соответствия ƒ и g, изображенные на рисунке 98 а и б, являются функциями, а на рисунке 98 в и г - нет. В случае в - не каждому элементу хÎX соответствует элемент уÎY. В случае г не соблюдается условие однозначности.

Множество X называется областью определения функции ƒ и обозначается D(f). Множество всех уÎY называется множеством значений функции ƒ и обозначается Е(ƒ).

Числовые функции. График функции. Способы задания функций

Пусть задана функция ƒ : X→Y.

Если элементами множеств X и Y являются действительные числа (т. е. XÌ R и YÌ R), то функцию ƒ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=ƒ(х).

Переменная х называется при этом аргументом или независимой переменной, а у - функцией или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от х пишут в виде у=у(х), не вводя новой буквы (ƒ) для обозначения зависимости.

Частное значение функции ƒ(х) при х=a записывают так: ƒ(a). Например, если ƒ(х)=2х 2 -3, то ƒ(0)=-3, ƒ(2)=5.

Графиком функции у=(х) называется множество всех точек плоскости Оху, для каждой на которых х является значением аргумента, а у - соответствующим значением функции.

Например, графиком функции у=√(1-х 2) является верхняя полуокружность радиуса R=1 с центром в О(0;0) (см. рис. 99).

Чтобы задать функцию у=ƒ(х), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у.

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ : функция задается в виде одной или нескольких формул или уравнений.

Если область определения функции у = ƒ(х) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. Так, областью определения функции у= √(1-х2)является отрезок [-1; 1].

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию у=ƒ(х).

Графический способ: задается график функции.

Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.

Преимуществом графического задания является его наглядность, недостатком - его неточность.

Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.

На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.

Скачать с Depositfiles

Лекция № 9. Тема 3 : Линии второго порядка

Пусть в некоторой ДСК задана линия, определяемая уравнением второй степени

где коэффициенты
одновременно не равны нулю. Эта линия назы-вается кривой или линией второго порядка .

Может случиться, что нет точек
с действительными коорди-натами, удовлетворяющими уравнению (1). В этом случае считают, что уравнение (1) определяет мнимую линию второго порядка. Например,
 это уравнение мнимой окружности.

Рассмотрим три важных частных случаев уравнения (1).

3.1. Эллипс

Эллипс определяется уравнением

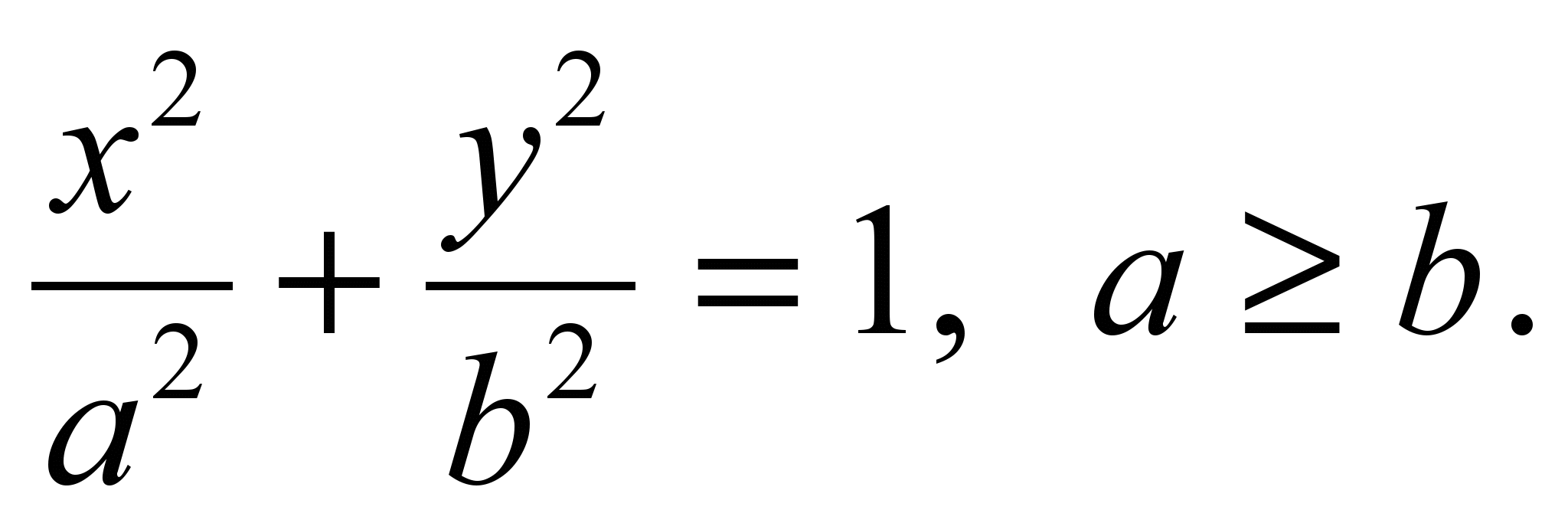(2)

Коэффициенты а и b называются соответственно большой и малой полуосями, а уравнение (2) – каноническим уравнением эллипса.

Положим
и отметим на оси Ох точки

называемые фокусами эллипса. Тогда эллипс можно определить как

геометрическое место точек, сумма расстояний от которых до фокусов есть величина постоянная, равная 2а .

M K

— а F 1 O F 2 a x

— b

Покажем это. Пусть точка
 текущая точка эллипса. В этом случае получаем Тогда должно выполняться равенство

Выражение (3) представим в виде

и возведём в квадрат обе части выражения

Отсюда получаем

Еще раз возведём это выражение в квадрат и воспользуемся соотно-шением
, тогда

(4)

Разделив обе части выражения (4) на
, окончательно получаем каноническое уравнение эллипса

Исследуем уравнение (2). Если в уравнении заменить , то уравнение (2) не изменится. Это означает, что эллипс симметричен относительно координатных осей. Поэтому рассмотрим подробно часть эллипса, находящуюся в первой четверти. Она определяется уравнением
Очевидно, что эллипс проходит через точки
. Выполнив схематическое построение в первой четверти, симметрично отобразим его график во все четверти. Таким образом, эллипс является непрерывной замкнутой кривой. Точки называются вершинами эллипса.

Отношение
называется эксцентриситетом эллипса. Для эллипса
.

Прямые
называются директрисами эллипса.

Справедливо следующее свойство директрис :

Отношение расстояний от фокуса и директрисы для точек эллипса есть величина постоянная, равная эксцентриситету, т.е.

Доказывается аналогично, как и равенство (3).

Замечание 1. Окружность
является частным случаем эллипса. Для неё

3.2. Гипербола

Каноническое уравнение гиперболы имеет вид

т.е. в уравнении (1) нужно положить

Коэффициенты а и b называются соответственно вещественной и мнимой полуосями.

Положив
, отметим на оси Ох точки
на-зываемые фокусами гиперболы. Тогда гиперболу можно определить как

геометрическое место точек, разность расстояний от которых до фокусов по абсолютной величине равна 2 а , т.е.

К М

F 1 —а О а F 2 х

Доказывается аналогично, как и для эллипса. По виду уравнения гиперболы так же заключаем, что её график симметричен относительно осей системы координат. Часть гиперболы, лежащая в первой четверти, имеет уравнение
Из этого уравнения видно, что при достаточно больших х гипербола близка к прямой
. После схематичного построения в первой четверти симметрично отобра-жаем график во все четверти.